
SPEED OF SOUND EQUATION CODE
Whether your PC or MAC can display a particular code is another question, with the answer depending on the fonts available and the characters supported by any particular font.īy the way, character sets for which codes have recently been defined include Game Tiles, Egyptian Heiroglyphics, Phoenician and Phags-pa.

The number of characters for which codes are defined is still growing, but few, if any charaters are yet assigned codes that require more than 16 bits. This could permit up to 4294967296 characters in principle, although for technical reasons not all code positions are available for distinct characters. In its fullest form, this uses 32 bits to encode characters. These days, most modern computer systems use use Unicode (or ISO/IEC 10646, which is essentially the same thing) for character coding. I don't know what, if any, is the limit these days but the sets have heaps and heaps of characters. This little utility allows you to copy and paste any character into your application, including a bunch of math symbols. The speed of sound is affected by temperature in a given medium.These days, the easiest way (in Windows) is to run the charmap program - see the previous post for the location. The time between the P- and S-waves is routinely used to determine the distance to their source that is, the epicenter of the earthquake. The P-wave gets progressively farther ahead of the S-wave as they travel through Earth’s crust. P-waves have speeds of 4 to 7 km/s, and S-waves correspondingly range in speed from 2 to 5 km/s, both being faster in more rigid material. Both components of earthquakes travel slower in less rigid material, such as sediments. For that reason, the speed of longitudinal or pressure waves (P-waves) in earthquakes in granite is significantly higher than the speed of transverse or shear waves (S-waves). The faster a sound wave travels, the more distance it will cover in the same period of time. The bulk modulus of granite is greater than its shear modulus. Earthquakes have both longitudinal and transverse components, and these travel at different speeds.

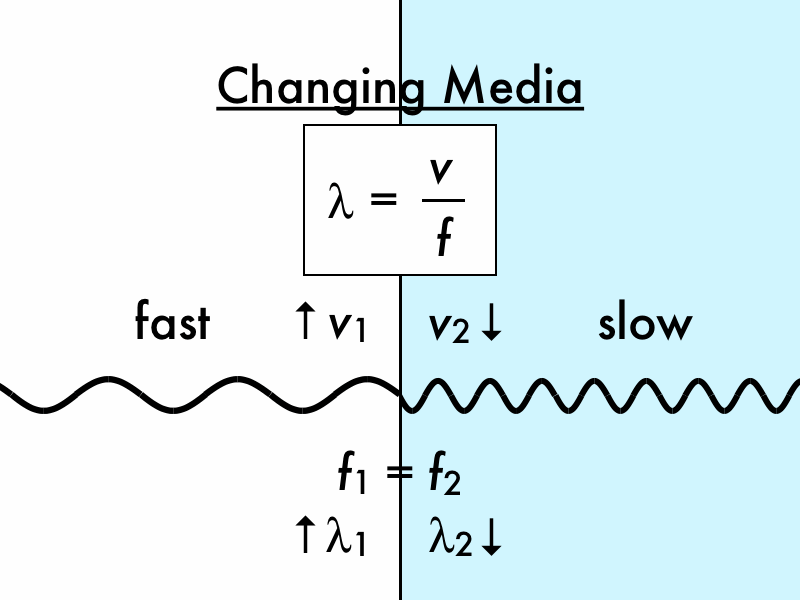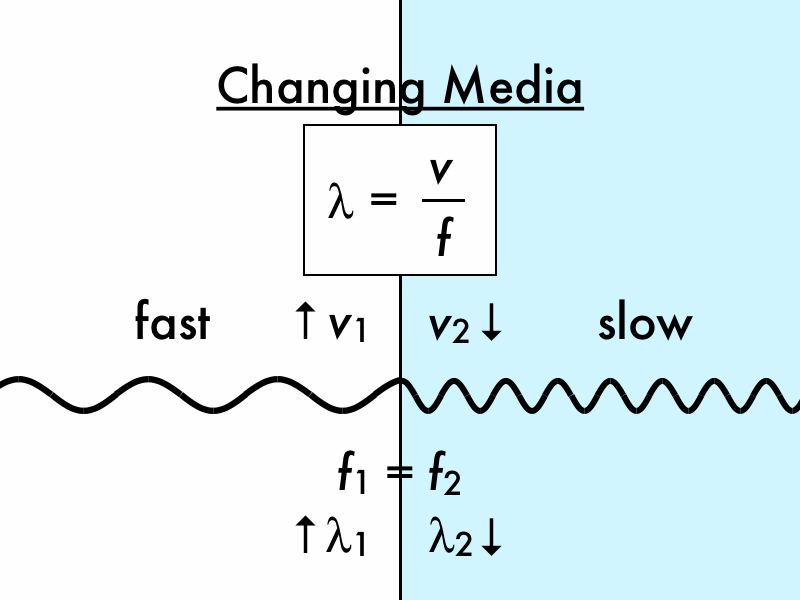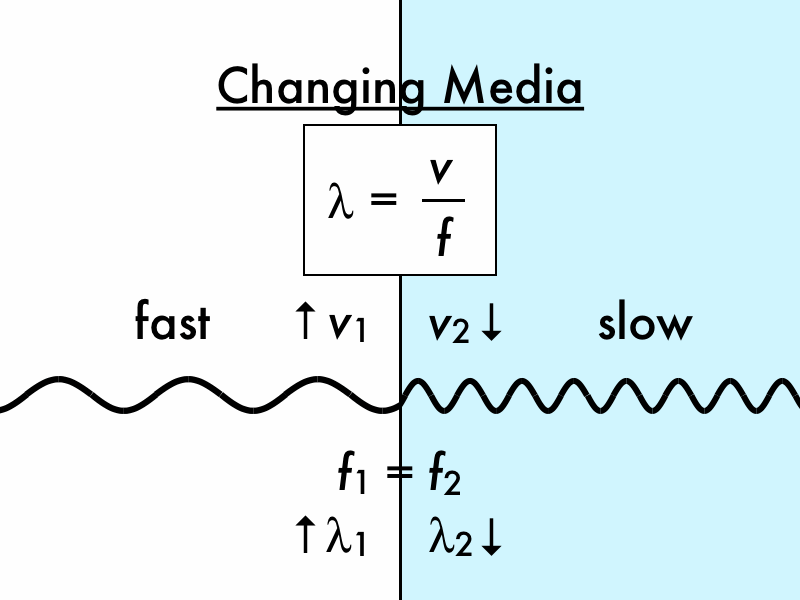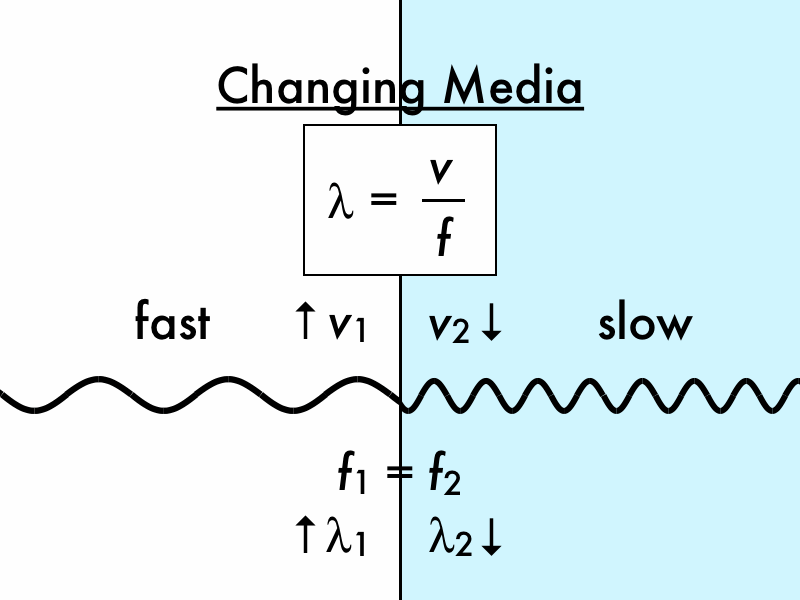
Table 17.4 Speed of Sound in Various MediaĮarthquakes, essentially sound waves in Earth’s crust, are an interesting example of how the speed of sound depends on the rigidity of the medium. Sound travels from one point to another in the form of waves and vibrations.These waves are audible mechanical waves, which are known as sound waves. Because liquids and solids are relatively rigid and very difficult to compress, the speed of sound in such media is generally greater than in gases. Speed of Sound varies depending upon the medium in which it travels. The speed of sound in air is low, because air is compressible. This observation is analogous to the fact that the frequency of a simple harmonic motion is inversely proportional to the mass of the oscillating object. The greater the density of a medium, the slower the speed of sound. This observation is analogous to the fact that the frequency of a simple harmonic motion is directly proportional to the stiffness of the oscillating object. The more rigid (or less compressible) the medium, the faster the speed of sound. The speed of sound in a medium is determined by a combination of the medium’s rigidity (or compressibility in gases) and its density. Table 17.4 makes it apparent that the speed of sound varies greatly in different media. The relationship of the speed of sound, its frequency, and wavelength is the same as for all wavesįigure 17.9 A sound wave emanates from a source vibrating at a frequency f, f, propagates at Similar arguments hold that a large instrument creates long-wavelength sounds. So a small instrument creates short-wavelength sounds. High pitch means small wavelength, and the size of a musical instrument is directly related to the wavelengths of sound it produces. Small instruments, such as a piccolo, typically make high-pitch sounds, while large instruments, such as a tuba, typically make low-pitch sounds. The wavelength of sound is not directly sensed, but indirect evidence is found in the correlation of the size of musical instruments with their pitch. You can also directly sense the frequency of a sound.

The flash of an explosion is seen well before its sound is heard, implying both that sound travels at a finite speed and that it is much slower than light. You can observe direct evidence of the speed of sound while watching a fireworks display. Sound, like all waves, travels at a certain speed and has the properties of frequency and wavelength. Sound travels more slowly than light does. Figure 17.8 When a firework explodes, the light energy is perceived before the sound energy.


 0 kommentar(er)
0 kommentar(er)
